The NTP Timescale and Leap Seconds

Last update: June 24, 2022 20:19 UTC (fc65ae47b)

gif

from Alice’s Adventures in Wonderland, Lewis Carroll

The Mad Hatter and the March Hare are discussing whether the Teapot serial number should have two or four digits.

Table of Contents

Abstract

The timescale used by the Network Time Protocol (NTP) is based on coordinated univeral time (UTC), which itself is based on the Earth rotation about its axis. As the rotation of the Earth is slowing very gradually, this requires a leap second to be inserted in the timescale at approximately eighteen month intervals. This document describes the mechanics of insertion and how it affects the timescale shortly before, during and after the leap second.

Introduction

The conventional civil timescale used in most parts of the world is based on Coordinated Universal Time (UTC sic). The rate of UTC is based on International Atomic Time (TAI sic), which is derived from hundreds of cesium and hydrogen clocks in the national standards laboratories of many countries. The UTC timescale is derived from the UT1 timescale, which is based on the rotation of Earth about its axis. Corrections of UTC relative to UT1 are implemented in the form of leap seconds, which occur at intervals from several months to several years. This document considers what happens in the NTP timescale upon the epoch of a leap second and how and why it differs from conventional Unix models such as POSIX.

While TAI is useful in the scientific community, most of us reckon time according to the Sun and season. Starting from TAI, the UT0 timescale is determined using corrections for Earth orbit and inclination (the Equation of Time as used by sundials). The International Earth Rotation Service (IERS) at the Paris Observatory uses astronomical observations provided by USNO and other observatories to determine the UT1 (navigator’s) timescale corrected for irregular variations in Earth rotation.

How UTC Reckons with Leap Seconds

While UT1 defines the solar day, adopting it would require resetting our clocks some fraction of a second every month or two. On the epoch 0h 1 January 1972, UTC was defined TAI - 10 s, within 0.5 s of UT1, but the offset TAI - UT1 has been slowly increasing since then; in mid 2007 it is 33 s. When the offset UT1 - UTC becomes greater than about 0.5 s, a leap second is inserted in the UTC timescale. The residual difference is called the DUT1 correction in broadcast timecode formats and is represented in deciseconds (0.1 s).

For the most precise coordination and timestamping of events since 1972, it is necessary to know when leap seconds were implemented in UTC and how the seconds are numbered. This is currently the responsibility of the IERS, which publishes periodic bulletins available on the Internet. As specified in CCIR Report 517 and later revised, a leap second is inserted following second 23:59:59 on the last day of any designated month and becomes second 23:59:60 of that day. A leap second would be deleted by omitting second 23:59:59 on one of these days, although this has never happened.

A record of leap seconds, both historic and anticipated, is included in the NIST Time Scale Data Archive, which has been updated on a monthly basis since UTC began in 1972. A computer-readable summary is available in the leap-seconds.list file, which includes the NTP time of each leap second, along with the TAI-UTC offset. A specimen leap-seconds.list file is shown in Appendix A.

The UTC timescale thus ticks in standard SI seconds and was set TAI - 10 s at 0h Modified Julian Day (MJD) 41,317.5 according to the Julian-day calendar or 0h 1 January 1972 according to the Gregorian calendar. This established the first tick of the UTC era and its reckoning with these calendars. Subsequently, the UTC timescale has marched backward relative to the TAI timescale exactly one second on scheduled occasions recorded in the institutional memory of our civilization.

Note in passing that leap second adjustments affect the number of seconds per day and thus the number of seconds per year. Apparently, should we choose to worry about it, the UTC clock, Gregorian calendar and various cosmic oscillators will inexorably drift apart with time until rationalized by a future papal bull.

While of less use to the computer timekeeper, the Global Positioning System (GPS), which is widely used to disseminate standard time, has its own timescale. The GPS timescale is syntonic with TAI, but at a fixed time offset of -19 s from TAI, apparently because the final system design review was in 1980. GPS reference clocks typically convert from GPS to UTC for external readings.

How NTP and POSIX Reckon with Leap Seconds

The NTP and POSIX timescales are based on the UTC timescale, but not always coincident with it. The origin of the NTP timescale, the prime epoch, is 0h 1 January 1900, while the prime epoch of the POSIX timescale is 0h 1 January 1970. Both timescales reckon in standard (SI) seconds since the prime epoch. For instance, upon the first tick of UTC on 0h 1 January 1972 the NTP clock read 2,272,060,800, representing the number of SI seconds since the prime epoch.

The insertion of leap seconds in UTC and subsequently into NTP and POSIX affect the system clock, and thus the conversion between system clock time and conventional civil time in hours, minutes and seconds. However, since the only institutional memory available to determine the conversion are the UTC national broadcast services, the conversion is in effect reset to UTC as each broadcast timecode is received. Thus, when a leap second is inserted in UTC and subsequently in NTP or POSIX, knowledge of all previous leap seconds is lost.

Another way to describe this is to say there are as many NTP or POSIX timescales as historic leap seconds. In effect, a new timescale is reestablished after each new leap second. Thus, all previous leap seconds, not to mention the apparent origin of the timescale itself, lurch backward one second as each new timescale is established. For instance, if a clock synchronized to UTC in 2005 was used to establish the UTC epoch of an event that occurred in early 1972 without correction, the event would appear 22 seconds late. As a result, for the most precise determination of epoch relative to the historic Gregorian calendar and UTC timescale, the user must subtract from the apparent NTP or POSIX epoch the relevant offset provided by the IERS. This is a feature of almost all present day time distribution mechanisms.

How NTP and POSIX Number the Seconds

There are three approaches to implementing a leap second. The first approach is to increment the system clock during the leap second and continue incrementing following the leap. The problem with this approach is that conversion to UTC requires knowledge of all past leap seconds and epoch of insertion. The second approach is to increment the system clock during the leap second and step the clock backward one second at the end of the leap second. This is the approach taken by the POSIX conventions. The problem with this approach is that the resulting timescale is discontinuous and ambiguous, since a reading during the leap is repeated one second later. The third approach is to freeze the clock during the leap second allowing the time to catch up at the end of the leap second. This is the approach taken by the NTP conventions.

The NTP conventions are based on a set of formal assertions suggested by the computer science theory community.

The detailed chronometry with either of the POSIX or NTP conventions is illustrated in Table 1. It shows the seconds numbering at the beginning of the second just before, during and just after the leap second at 23:59:59 UTC on 31 December 1998.

Date Time TAI Offset NTP Leap NTP Seconds
31 Dec 98 23:59:59 31 01 3,124,137,599
23:59:60 31 01 3,124,137,600
1 Jan 99 00:00:00 32 00 3,124,137,600
00:00:01 32 00 3,124,137,601

Table 1. NTP Leap Second Numbering

While the last second of a normal day is 23:59:59, the last second of a leap day is 23:59:60. Since this makes the day one second longer than the usual day, the day rollover will not occur until the end of the first occurrence of second 3,124,137,600.

Note that the NTP Seconds column in Table 1 actually shows the epoch of the leap second itself, which is the precise epoch of insertion. The TAI Offset column shows the cumulative seconds offset of UTC relative to TAI; that is, the number of seconds to add to UTC in order to maintain nominal agreement with TAI.

Finally, note that the epoch of insertion is relative to the timescale immediately prior to that epoch; e.g., the epoch of the 31 December 1998 insertion is determined on the timescale in effect just prior to this insertion, which means the actual insertion relative to TAI is 21 seconds earlier than the apparent time on the UTC timescale.

How NTP Implements Leap Seconds

The obvious question raised by the NTP conventions is what happens during the leap second itself when NTP time stops and the clock remains unchanged. The NTP leap bits are set on the leap day, either directly by a reference clock driver or indirectly by the protocol. The leap second is implemented at the end of the normal day of 86,400 s, then the leap bits are reset.

If the precision time kernel modifications have been implemented, the kernel includes a state machine that implements the actions required by the scenario. The state machine implemented in most recent Unix kernels is described in the nanokernel software distribution. At the first occurrence of second 3,124,137,600, the system clock is stepped backward one second. The operating system kernel time conversion routines can recognize this condition and show the leap second as number 60.

However, the routine that actually reads the clock is constrained never to step backwards, unless the step is significantly larger than one second, which might occur due to explicit operator direction. In this design time stands still during the leap second, but is correct commencing with the next second.

gif

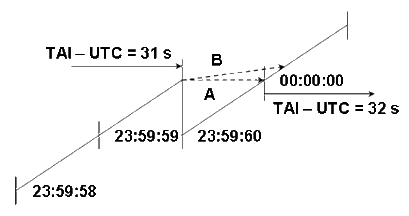
Figure 1. NTP Offset In the Vicinity of a Leap Second

Figure 1 shows the behavior with the modified design used in most kernels. Unlike the POSIX conventions, the NTP clock is frozen and does not advance during the leap second, so there is no need to set it back one second at the end of the leap second. The chronometric correspondence between the UTC and NTP timescales continues, but NTP has forgotten about all past leap insertions. Thus, determination of UTC time intervals spanning leap seconds will be in error, unless the exact times of insertion are known from the NIST table and its successors.

Immediately after the leap second insertion, both timescales resume ticking the seconds as if the leap had never happened. The clock reading is constrained to always increase, so every reading during the leap second increases the NTP clock by at least one microsecond for older kernels and one nanosecond for newer ones.

In case A the clock was not read during the leap second, so appears to stand still. In case B the clock was read one or more times during the leap second, so the value increments beyond the last reading. This will persist until after the leap second the stepped-back clock catches up to this value.

Parting Shots

There might be some concern about the possibility of a software hazard which attempts to read the system clock as fast as possible. In principle, this could lead to a large divergence between the clock reading and the actual time, and that could grow indefinitely. With a modern nanosecond kernels and a typical time to read the system clock of 100 ns, the divergence at the end of the leap second would be no more than 10 ms. On the other hand, with an older microsecond kernel and a typical time to read the system clock of 1000 ns, the divergence after the leap second could be as much as one second. Means should be provided to protect against this kind of hazard.

Appendix A. Specimen NIST leap-seconds.list File

The following is a verbatim copy of a specimen leap seconds.list file available from most NIST time servers. The file name is a link to the actual file name with extension depending on the file generation, such as leap-seconds.

#
#	In the following text, the symbol '#' introduces
#	a comment, which continues from that symbol until
#	the end of the line. A plain comment line has a
#	whitespace character following the comment indicator.
#	There are also special comment lines defined below.
#	A special comment will always have a non-whitespace
#	character in column 2.
#
#	A blank line should be ignored.
#
#	The following table shows the corrections that must
#	be applied to compute International Atomic Time (TAI)
#	from the Coordinated Universal Time (UTC) values that
#	are transmitted by almost all time services.
#
#	The first column shows an epoch as a number of seconds
#	since 1900.0 and the second column shows the number of
#	seconds that must be added to UTC to compute TAI for
#	any timestamp at or after that epoch. The value on
#	each line is valid from the indicated initial instant
#	until the epoch given on the next one or indefinitely
#	into the future if there is no next line.
#	(The comment on each line shows the representation of
#	the corresponding initial epoch in the usual
#	day-month-year format. The epoch always begins at
#	00:00:00 UTC on the indicated day. See Note 5 below.)
#	
#	Important notes:
#
#	1. Coordinated Universal Time (UTC) is often referred to
#	as Greenwich Mean Time (GMT). The GMT time scale is no
#	longer used, and the use of GMT to designate UTC is
#	discouraged.
#
#	2. The UTC time scale is realized by many national
#	laboratories and timing centers. Each laboratory
#	identifies its realization with its name: Thus
#	UTC(NIST), UTC(USNO), etc. The differences among
#	these different realizations are typically on the
#	order of a few nanoseconds (i.e., 0.000 000 00x s)
#	and can be ignored for many purposes. These differences
#	are tabulated in Circular T, which is published monthly
#	by the International Bureau of Weights and Measures
#	(BIPM). See www.bipm.fr for more information.
#
#	3. The current definition of the relationship between UTC
#	and TAI dates from 1 January 1972. A number of different
#	time scales were in use before than epoch, and it can be
#	quite difficult to compute precise timestamps and time
#	intervals in those prehistoric days. For more information,
#	consult:
#
#		The Explanatory Supplement to the Astronomical
#		Ephemeris.
#	or
#		Terry Quinn, The BIPM and the Accurate Measurement
#		of Time, Proc. of the IEEE, Vol. 79, pp. 894-905,
#		July, 1991.
#
#	4.  The insertion of leap seconds into UTC is currently the
#	responsibility of the International Earth Rotation Service,
#	which is located at the Paris Observatory:
#
#	Central Bureau of IERS
#	61, Avenue de l'Observatoire
#	75014 Paris, France.
#
#	Leap seconds are announced by the IERS in its Bulletin C
#
#	See hpiers.obspm.fr or www.iers.org for more details.
#
#	All national laboratories and timing centers use the
#	data from the BIPM and the IERS to construct their
#	local realizations of UTC.
#
#	Although the definition also includes the possibility
#	of dropping seconds (negative leap seconds), this has
#	never been done and is unlikely to be necessary in the
#	foreseeable future.
#
#	5. If your system keeps time as the number of seconds since
#	some epoch (e.g., NTP timestamps), then the algorithm for
#	assigning a UTC time stamp to an event that happens during a positive
#	leap second is not well defined. The official name of that leap
#	second is 23:59:60, but there is no way of representing that time
#	in these systems.
#	Many systems of this type effectively stop the system clock for
#	one second during the leap second and use a time that is equivalent
#	to 23:59:59 UTC twice. For these systems, the corresponding TAI
#	timestamp would be obtained by advancing to the next entry in the
#	following table when the time equivalent to 23:59:59 UTC
#	is used for the second time. Thus the leap second which
#	occurred on 30 June 1972 at 23:59:59 UTC would have TAI
#	timestamps computed as follows:
#
#	...
#	30 June 1972 23:59:59 (2287785599, first time):	TAI= UTC + 10 seconds
#	30 June 1972 23:59:60 (2287785599,second time):	TAI= UTC + 11 seconds
#	1  July 1972 00:00:00 (2287785600)		TAI= UTC + 11 seconds
#	...
#
#	If your system realizes the leap second by repeating 00:00:00 UTC twice
#	(this is possible but not usual), then the advance to the next entry
#	in the table must occur the second time that a time equivalent to
#	00:00:00 UTC is used. Thus, using the same example as above:
#
#	...
#       30 June 1972 23:59:59 (2287785599):		TAI= UTC + 10 seconds
#       30 June 1972 23:59:60 (2287785600, first time):	TAI= UTC + 10 seconds
#       1  July 1972 00:00:00 (2287785600,second time):	TAI= UTC + 11 seconds
#	...
#
#	in both cases the use of timestamps based on TAI produces a smooth
#	time scale with no discontinuity in the time interval.
#
#	This complexity would not be needed for negative leap seconds (if they
#	are ever used). The UTC time would skip 23:59:59 and advance from
#	23:59:58 to 00:00:00 in that case.  The TAI offset would decrease by
#	1 second at the same instant.  This is a much easier situation to deal
#	with, since the difficulty of unambiguously representing the epoch
#	during the leap second does not arise.
#
#	Questions or comments to:
#		Judah Levine
#		Time and Frequency Division
#		NIST
#		Boulder, Colorado
#		jlevine@boulder.nist.gov
#
#	Last Update of leap second values:   8 August 2008
#
#	The following line shows this last update date in NTP timestamp
#	format. This is the date on which the most recent change to
#	the leap second data was added to the file. This line can
#	be identified by the unique pair of characters in the first two
#	columns as shown below.
#
#$	 3427142400
#
#	The NTP timestamps are in units of seconds since the NTP epoch,
#	which is 1900.0. The Modified Julian Day number corresponding
#	to the NTP time stamp, X, can be computed as
#
#	X/86400 + 15020
#
#	where the first term converts seconds to days and the second
#	term adds the MJD corresponding to 1900.0. The integer portion
#	of the result is the integer MJD for that day, and any remainder
#	is the time of day, expressed as the fraction of the day since 0
#	hours UTC. The conversion from day fraction to seconds or to
#	hours, minutes, and seconds may involve rounding or truncation,
#	depending on the method used in the computation.
#
#	The data in this file will be updated periodically as new leap
#	seconds are announced. In addition to being entered on the line
#	above, the update time (in NTP format) will be added to the basic
#	file name leap-seconds to form the name leap-seconds.
#	In addition, the generic name leap-seconds.list will always point to
#	the most recent version of the file.
#
#	This update procedure will be performed only when a new leap second
#	is announced.
#
#	The following entry specifies the expiration date of the data
#	in this file in units of seconds since 1900.0.  This expiration date
#	will be changed at least twice per year whether or not a new leap
#	second is announced. These semi-annual changes will be made no
#	later than 1 June and 1 December of each year to indicate what
#	action (if any) is to be taken on 30 June and 31 December,
#	respectively. (These are the customary effective dates for new
#	leap seconds.) This expiration date will be identified by a
#	unique pair of characters in columns 1 and 2 as shown below.
#	In the unlikely event that a leap second is announced with an
#	effective date other than 30 June or 31 December, then this
#	file will be edited to include that leap second as soon as it is
#	announced or at least one month before the effective date
#	(whichever is later).
#	If an announcement by the IERS specifies that no leap second is
#	scheduled, then only the expiration date of the file will
#	be advanced to show that the information in the file is still
#	current -- the update time stamp, the data and the name of the file
#	will not change.
#
#	Updated through IERS Bulletin C41
#	File expires on:  28 Dec 2011
#
#@	3534019200
#
2272060800	10	# 1 Jan 1972
2287785600	11	# 1 Jul 1972
2303683200	12	# 1 Jan 1973
2335219200	13	# 1 Jan 1974
2366755200	14	# 1 Jan 1975
2398291200	15	# 1 Jan 1976
2429913600	16	# 1 Jan 1977
2461449600	17	# 1 Jan 1978
2492985600	18	# 1 Jan 1979
2524521600	19	# 1 Jan 1980
2571782400	20	# 1 Jul 1981
2603318400	21	# 1 Jul 1982
2634854400	22	# 1 Jul 1983
2698012800	23	# 1 Jul 1985
2776982400	24	# 1 Jan 1988
2840140800	25	# 1 Jan 1990
2871676800	26	# 1 Jan 1991
2918937600	27	# 1 Jul 1992
2950473600	28	# 1 Jul 1993
2982009600	29	# 1 Jul 1994
3029443200	30	# 1 Jan 1996
3076704000	31	# 1 Jul 1997
3124137600	32	# 1 Jan 1999
3345062400	33	# 1 Jan 2006
3439756800	34	# 1 Jan 2009
#
#	the following special comment contains the
#	hash value of the data in this file computed
#	use the secure hash algorithm as specified
#	by FIPS 180-1. See the files in ~/sha for
#	the details of how this hash value is
#	computed. Note that the hash computation
#	ignores comments and whitespace characters
#	in data lines. It includes the NTP values
#	of both the last modification time and the
#	expiration time of the file, but not the
#	white space on those lines.
#	the hash line is also ignored in the
#	computation.
#
#	465a56fc 6c72f658 f1fe29c8 eec831a4 e19b5438